2023下半年“深圳杯”数学建模竞赛、“东三省”数学建模竞赛的比赛已经开启，8月初“华数杯”全国大学生数学建模竞赛即将开始、9月份“高教社杯”全国大学生数学建模竞赛等等。很多同学都是第一次参加数学建模比赛，

　　评价模型用于对某个系统、方案或决策进行评估。通过构建合适的指标和评价方法，评价模型能够对不同方案的优劣进行比较和分析。在数学建模比赛中，评价模型通常根据问题的特点和需求，设计合适的评价标准和指标，对不同方案或模型的性能进行评估和比较，以帮助做出决策。

　　预测模型能够根据过去的数据和观察结果，对未来的趋势、行为或结果进行预测和推断。预测模型常用于分析时间序列数据、趋势预测、行为模式预测等问题。在数学建模比赛中，预测模型可以根据给定的数据集或者特定规律，构建合适的数学模型，进行未来趋势预测，从而帮助做出决策或规划。

　　优化模型旨在找到使某个目标函数取得最大或最小值的最优解。优化模型适用于求解最佳决策、资源分配、排产安排等问题。在数学建模比赛中，优化模型可以通过建立数学规划模型，确定决策变量、约束条件和目标函数，利用求解方法寻找最优解或次优解，以优化问题的方案或决策。

　　数理统计模型用于对数据进行分析、总结和推断。它能够通过建立概率模型和统计分布，对数据的特征、关系和不确定性进行描述和推断。在数学建模比赛中，数理统计模型可以通过对给定数据集的统计分析，推断出数据的分布规律、相关性、假设检验等，为问题提供支持和解决方案。

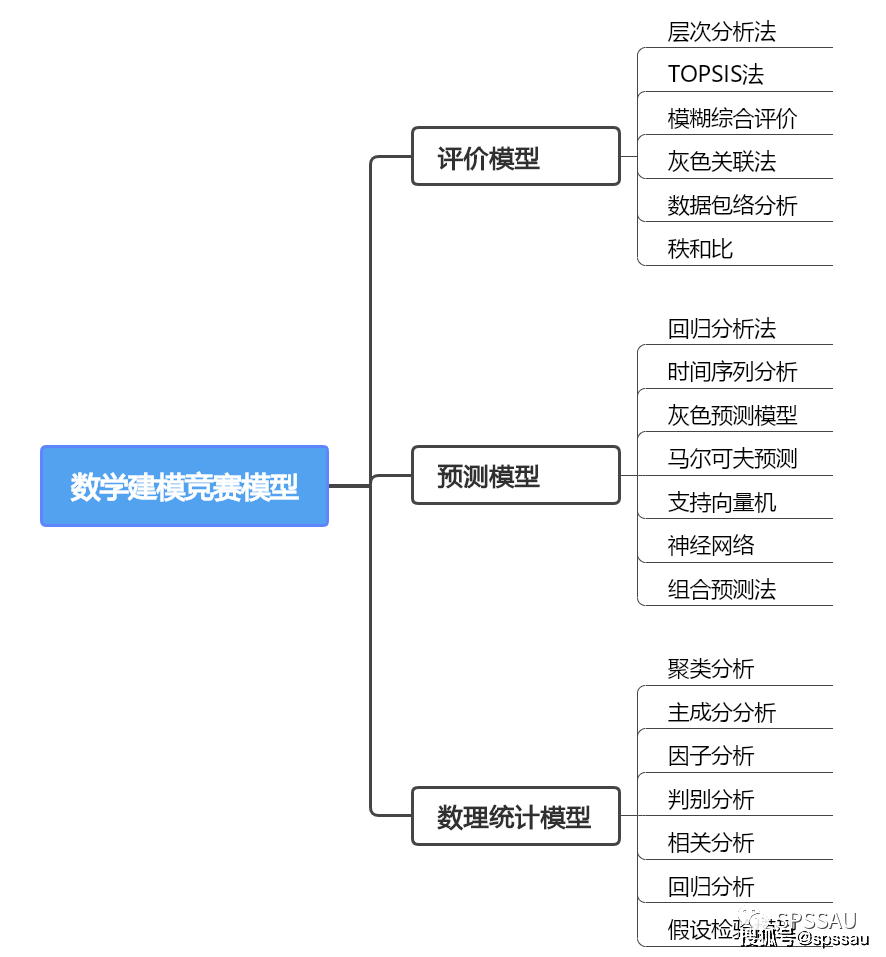
　　AHP层次分析法是一种解决多目标复杂问题的定性和定量相结合进行计算决策权重的研究方法。它通过构建层次结构，将复杂的决策问题分解成多个层次，并使用专家判断和比较来确定各个因素的权重，从而得出最终决策结果。比较有效地应用于那些难以用定量方法解决的课题。

　　AHP层次分析法包括两个步骤，分别是权重计算和一致性检验（SPSSAU会默认输出）；

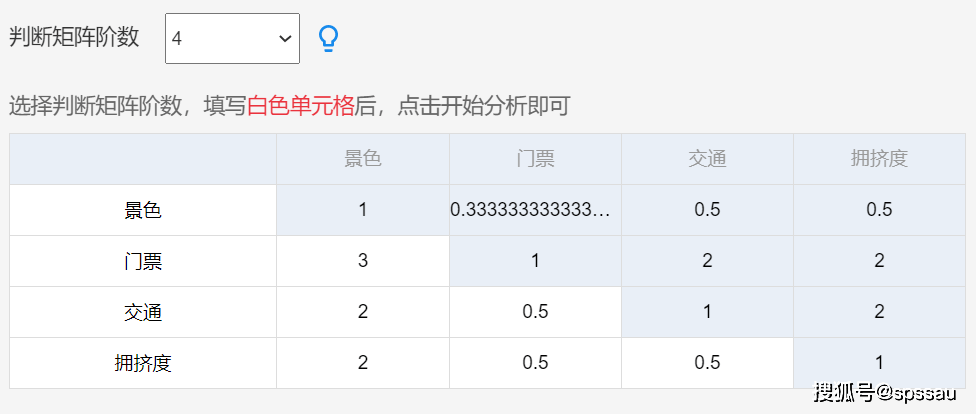
　　判断矩阵解读：门票相对于景色来讲，重要性更高，所以为3分；相反，景色相对于门票来讲，则为0.33333分。交通相对于景色来更重要为2分，其余类似下去。

　　TOPSIS法是一种基于距离和相似性度量的多属性决策方法。TOPSIS法首先将多个备选方案与理想解进行比较，计算每个备选方案与理想解之间的相似性和距离。然后根据计算结果，评估和排序各个备选方案，选择最佳的方案。TOPSIS法能够较好地处理多属性决策问题，特别适用于需要考虑多个评价指标的情况。

　　第二步：数据归一化处理解决量纲问题（数据处理-生成变量，通常选择‘平方和归一化’）；

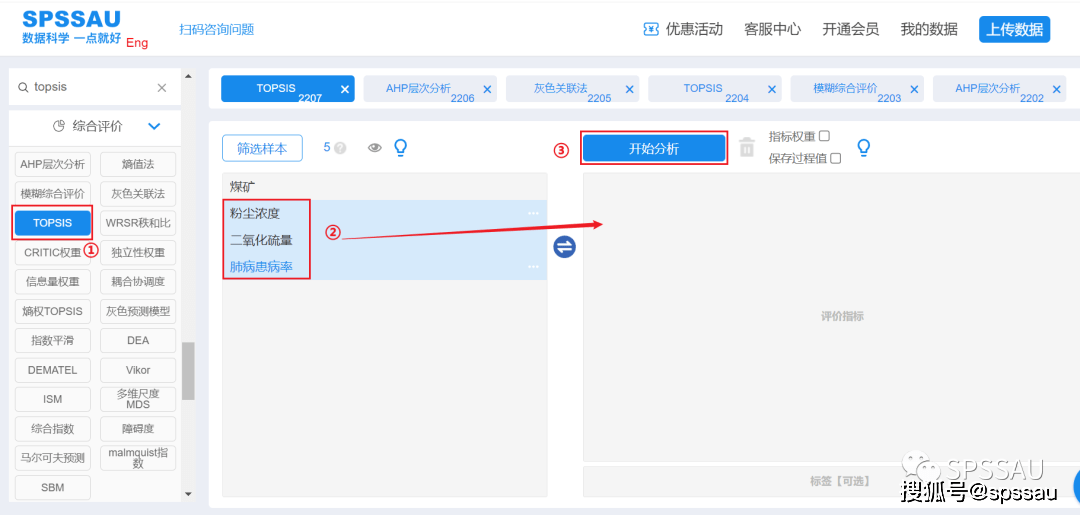
　　上传数据至SPSSAU系统，分析页面右侧选择【TOPSIS法】；将变量拖拽到右侧分析框中；点击“开始分析”，操作如下图：

　　模糊综合评价是一种处理具有模糊信息的评价方法。在模糊综合评价中，将模糊的评价指标通过隶属度函数转化为隶属度，然后根据权重给予不同指标不同的重要性。最后，通过对隶属度进行加权求和，得到一个综合评价结果。模糊综合评价方法能够有效处理不确定性和模糊性的问题，适用于现实世界中的复杂决策。

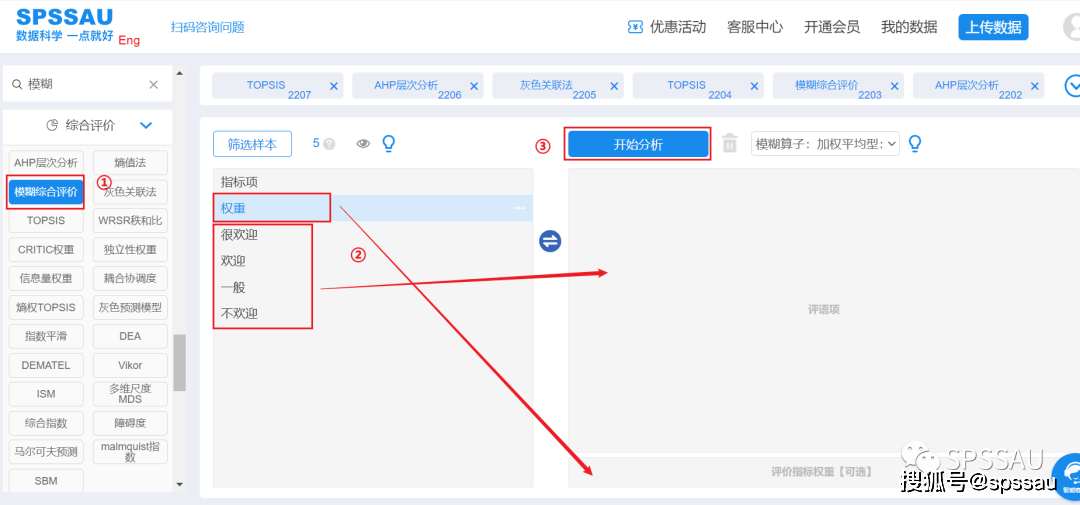
　　上传数据至SPSSAU系统，分析页面右侧选择【模糊综合评价】，将变量拖拽到右侧相应的分析框中，点击“开始分析”，操作图下图：

　　灰色关联分析法通过研究数据关联性大小（母序列与特征序列之间的关联程度），通过关联度（即关联性大小）进行度量数据之间的关联程度，从而辅助决策的一种研究方法。

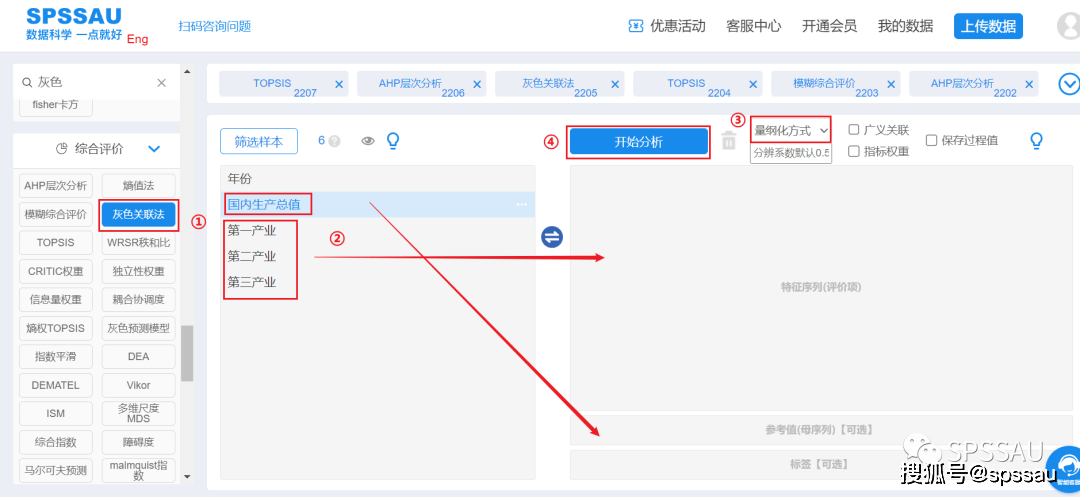
　　将数据上传至SPSSAU系统，分析页面右侧选择【灰色关联法】；将变量拖拽到右侧相应分析框中，选择“量纲化方式”，点击“开始分析”，操作如下图：

　　数据包络分析DEA是一种多指标投入和产出评价的研究方法。其应用数学规划模型计算比较决策单元（DMU）之间的相对效率，对评价对象做出评价。

　　数据包络分析DEA时，首先需要分析综合效益值θ，即首先判断DMU是否有DEA有效，如果有效，则说明该DMU较优，反之说明‘非DEA有效’，即相对来说还有提升空间，那么提升空间具体在哪里呢，比如提高还是减少规模呢，可以通过规模效益分析得到。与此同时，如果是‘非DEA有效’，那么具体问题是什么，投入冗余还是产出不足，则可以通过对应的投入冗余 或产出不足分析表格得出，具体数字直接查看松驰变量即可。澳门新葡萄新京APP

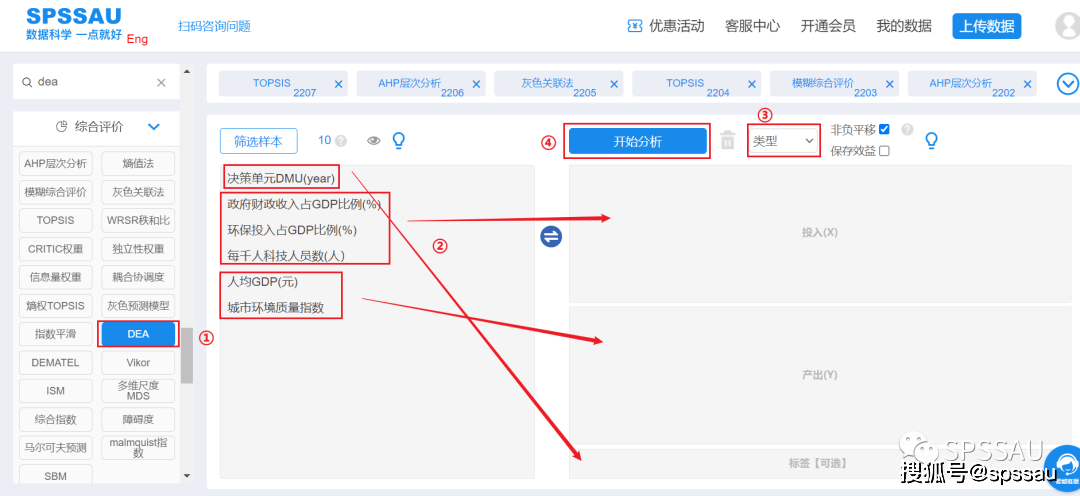
　　将数据上传至SPSSAU系统，分析页面右侧选择【DEA】，将变量拖拽到右侧相应分析框中，选择“DEA类型”，点击“开始分析”，操作如下图：

　　秩和比(RSR)方法是一种基于排序的模型比较方法。其实质原理是利用了RSR值信息进行各项数学计算，RSR值介于0~1之间且连续，通常情况下，该值越大说明评价越‘优’。

　　第一步：列出原始数据，一行代表一个评价对象，一列代表一个评价指标。最终为m*n矩阵；

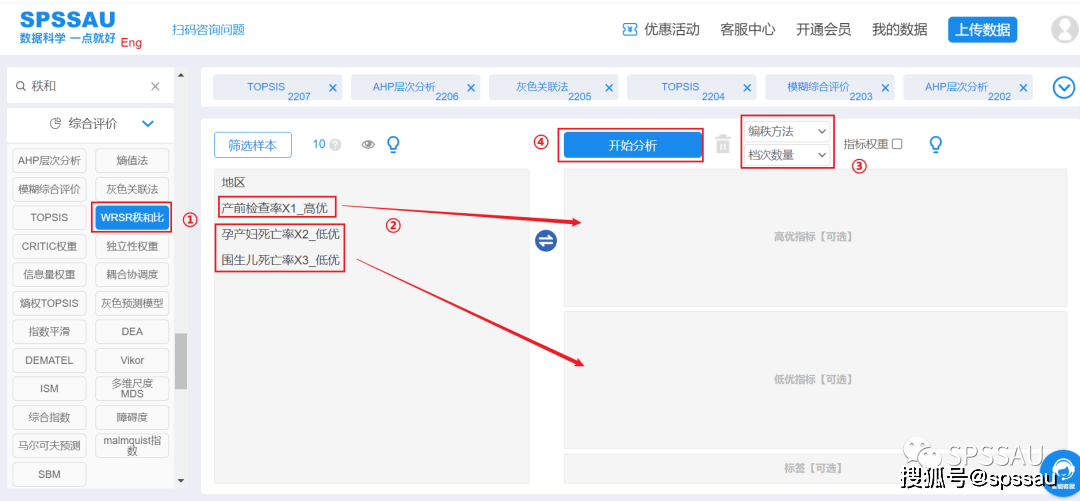
　　上传数据至SPSSAU系统，分析页面右侧选择【秩和比】，将变量拖拽到右侧相应分析框中，选择“编制方法”、“档次数量”，点击“开始分析”，操作如下图：

　　数学建模预测类模型通常用来根据现有数据和已知信息，进行未来事件、趋势或结果的预测和预估。这些模型通过分析历史数据、寻找规律和趋势，并由此推断未来的发展趋势和可能的结果。可以帮助人们做出合理判断、做出准确决策提供参考依据。

　　补充：组合预测法是一种将不同的预测模型或方法结合起来，以提高预测准确度和稳定性的方法。优势在于能够利用不同模型的长处，减少个别模型的局限性和不确定性带来的影响，提高预测的准确性和稳定性。常见的组合预测法有平均法、加权平均法、逐步加权法、组合模型法等。

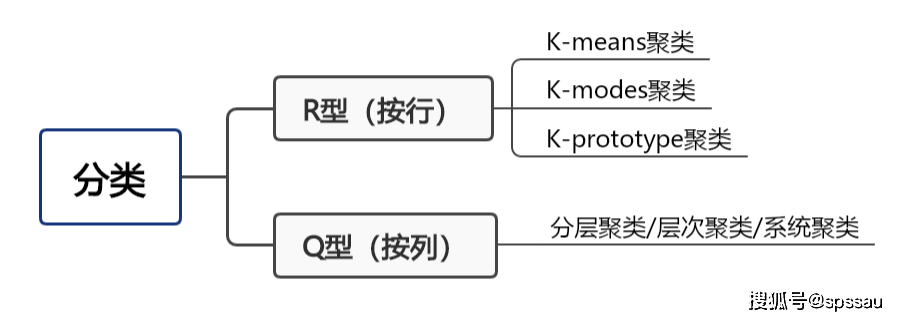
　　有关4种聚类分析算法相关知识，往期内容已经做过总结，感兴趣的同学可以自行查看。

　　主成分分析（PCA）是一种常用的数据降维和特征提取方法，它可以将具有相关性的多个变量转换为少数几个无关的主成分。这样可以简化复杂的数据结构，减少冗余信息，提高模型预测精度和解释能力，在数学建模中具有广泛的应用。

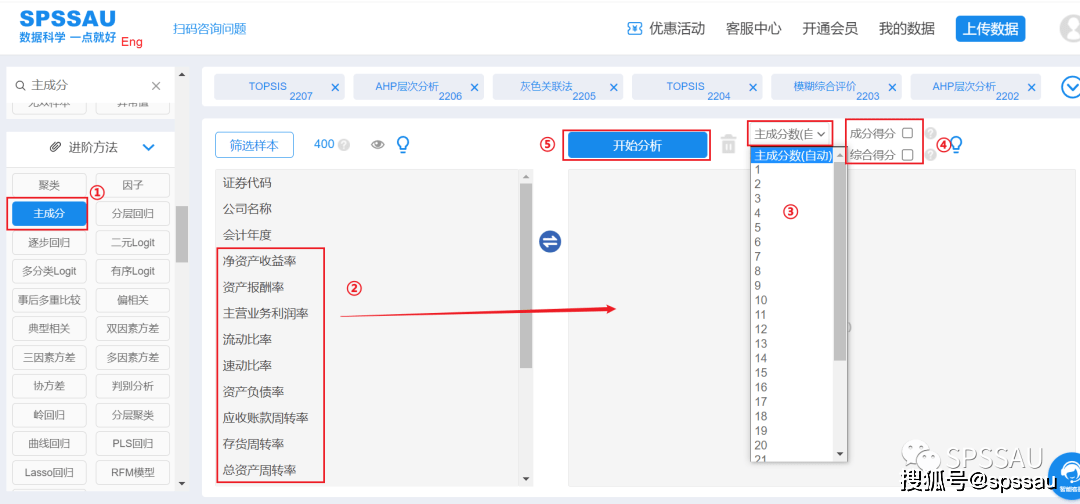
　　将数据上传至SPSSAU系统，分析页面右侧选择【主成分】；变量拖拽到右侧分析框中；选择“主成分个数”；根据分析目的选择勾选“成分得分”或“综合得分”；点击“开始分析”。

　　因子分析和主成分分析都是常用的数据降维方法，但它们的应用场景略有不同。主成分分析适合于变量之间相关性较高、需要提取重要变量或简化数据结构的情况；而因子分析适合于探索潜在因素、发现变量之间的共性或隐含关系的情况。选择哪种方法取决于具体的分析目的和数据特征。

　　判别分析(distinguish analysis)是一种机器学习算法，其用于在分类确定前提下，根据数据的特征研究数据归类问题。比如结合消费者的特征数据（比如消费金额、消费频次、购物时长、购买产品种类等），以预测消费者属于某种类型的顾客（款式偏好型、质量在乎型、价格敏感型等）。

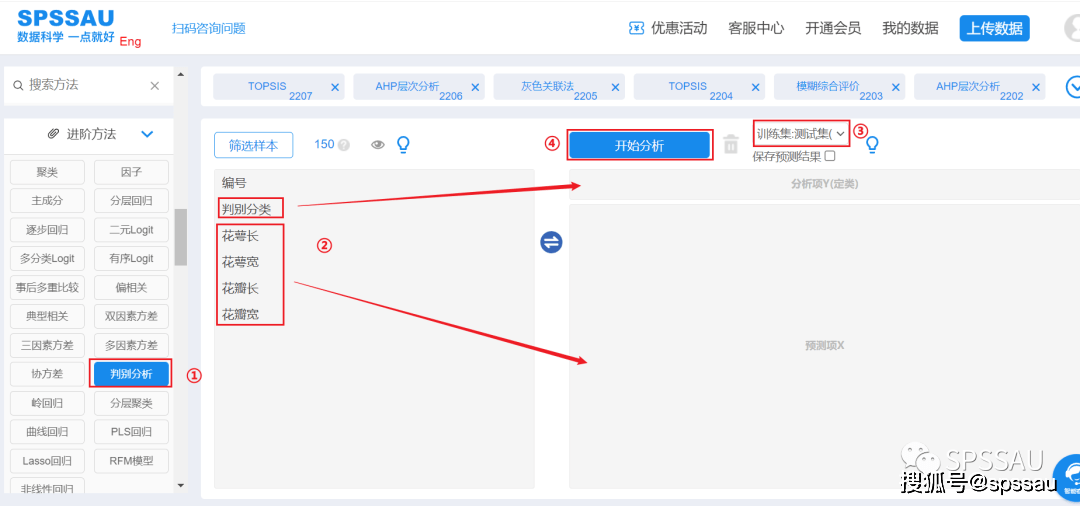
　　上传数据至SPSSAU系统，分析页面右侧选择【判别分析】；将变量拖拽到右侧相应分享框；选择“训练集:测试集”比例；点击“开始分析”，操作如下图：

　　相关分析用于分析变量之间的相关关系，包括是否有关系以及关系的紧密程度。在数学建模中，相关分析可用于衡量变量的关联性、选择变量、验证假设和推断、变量优化等。SPSSAU提供三类相关系数：Pearson系数、Spearman系数、Kendall协调系数。

　　第二步：判断关系为正相关或者负相关(相关系数大于0为正相关,反之为负相关)；

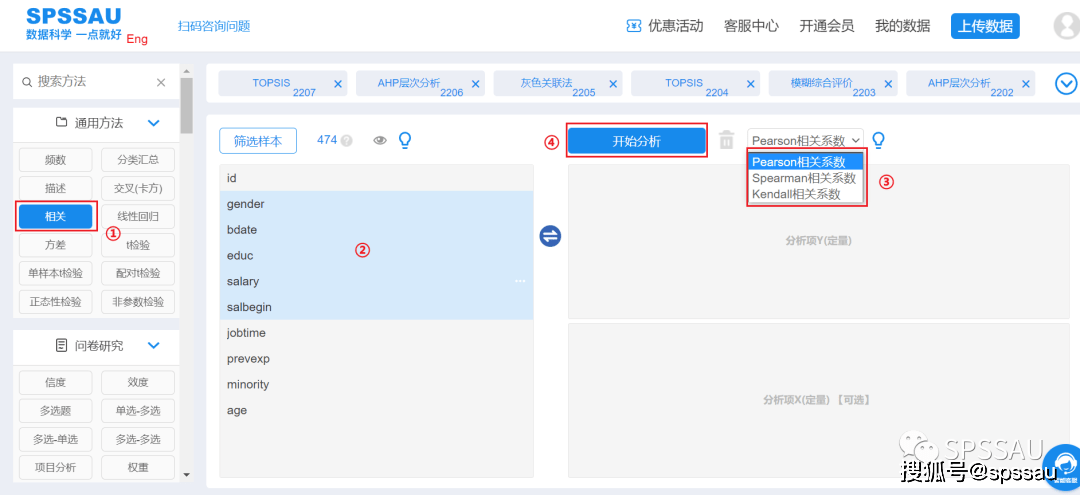
　　将数据上传至SPSSAU系统，分析页面右侧选择【相关】；将变量拖拽到右侧分析框中（可自由拖拽分析项进入分析列表框，区别仅在于输出格式不同）；选择“相关系数”；点击“开始分析”，操作如下图：

　　回归分析简单来讲就是用于分析自变量X与因变量Y之间的影响关系的方法。回归分析主要基于自变量X的值预测因变量Y的值，通过构造回归模型，帮助理解自变量如何影响因变量，以及各个自变量对因变量的影响程度。澳门新葡萄新京APP

　　回归分析可细分为20多种，常用的有多元线性回归、logistic回归、岭回归、逐步回归、lasso回归等。

　　数学建模中常用的假设检验模型包括t检验、方差分析、卡方检验、非参数检验等，它们可以用于判断样本和总体之间是否存在显著差异，以及变量之间是否存在相关性或影响关系。这些模型可以帮助我们验证研究假设，评估数据的可靠性和有效性，并帮助我们作出科学严谨的结论和决策。

　　使用SPSSAU进行数学建模竞赛可大大提高分析效率，对于第一次参加数学建模竞赛的小白，想要短期冲刺奖项也是非常不错的选择，感兴趣的同学可以试试看吧。返回搜狐，查看更多